喷泉取水问题（工程问题和相遇问题）

题面

有四个喷泉。

从第一个泉取一杯水，要用一天；

从第二个泉取一杯水，要用两天；

从第三个泉取一杯水，要用三天；

从第四个泉取一杯水，要用四天。

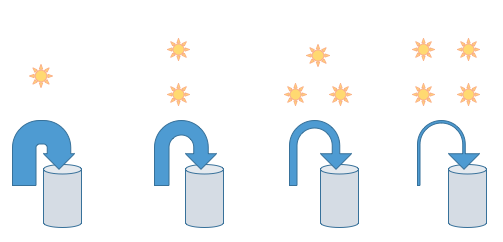
问：如果从四个泉同时向外引水，要用多长时间取一杯水？

换种问法

把杯子换成水池，把喷泉换成水龙头，题面变成：

有一个水池和四个水龙头。

只开第一个水龙头，要用一天灌满水池；

只开第一个水龙头，要用两天灌满水池；

只开第一个水龙头，要用三天灌满水池；

只开第一个水龙头，要用四天灌满水池。

问：四个水龙头一齐开，要用多长时间灌满？

再换种问法

把杯子换成路程，把喷泉换成甲和乙，题面变成：

有一段路程和甲乙两个人。

甲走完全程，要用一天；

乙走完全程，要用两天；

问：甲乙两个人相对着走，要用多长时间相遇？

题型总结

上面这些都是同一种类型的题目。可以总结为下面的类型：

有定量的资源，由多个消费者共同消费。

各个消费者有各自的消费速率，各不相同。所以当各个消费者独自消费整个资源时，会花费不同的时间。

消费者的速率有正有负。（消费速率为负时，即为生产者）

资源总量

总的资源量，是各个消费者要共同达成的目的，一般应该是动词+宾语的形式，比如：

• 完成一个项目
• 运走一堆沙子
• 填满一个池子
• 花完一笔款项

消费速率

这类题目有个重要的关系：

消费速率是个比值，是消费者消耗资源的份数

份数可能时间，也可能是物品的件数。是单位时间的量，也可能是单位个数的量。只要是单位的资源量就可以认为是速率。比如下面的概念都可以认为是消费速率：

• 消费者是杯子时，消费速率就是杯子每天装的水
• 消费者是工程队时，消费速率就是工程队每天干的活
• 消费者是运动者时，消费速率就是每天走的路程
• 消费者是物品时，消费速率就是每件物品的钱

上面的题解

定量的资源：填满杯子的容积

消费者：4个泉

每个泉消费的速率：

• 第一个泉：每天填满杯子容积
• 第二个泉：每天填满杯子容积的 $ \frac{1}{2} $
• 第三个泉：每天填满杯子容积的 $ \frac{1}{3} $
• 第四个泉：每天填满杯子容积的 $ \frac{1}{4} $

四个泉合作的消费速率为上面四个速率之和：每天填满杯子容积的 $ 1+ \frac{1}{2} + \frac{1}{3} + \frac{1}{4} $

合作所需的时间：

$$ t = \frac{1} {1+ \frac{1}{2} + \frac{1}{3} + \frac{1}{4}} = \frac{12}{25}天$$

如果您对本文有疑问或者寻求合作，欢迎 联系邮箱 。邮箱已到剪贴板

精彩评论