TL;DR
太长不看版:卷积是两个函数包含的信息糅合生成新函数的过程。
相互作用的例子
两个对等的事物相互作用、相互影响,你中有我,我中有你,最后形成的新事物,同时包含着原来双方的影子。比如:
- 整数乘法:
3 x 5 = 15
- 两幅图糅和成为一个新图:

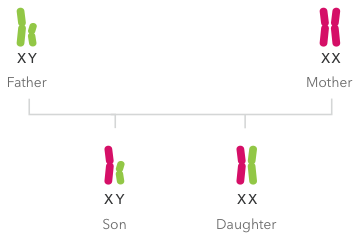
- 两套染色体合成一套新的染色体,孩子染色体上的每对基因,由父母的等位基因共同决定:
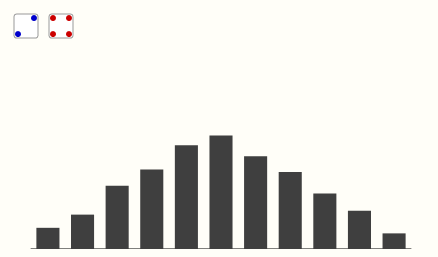
- 扔出两个骰子的点数之和 的概率。
字面含义
“卷积"并不是 convolution 的唯一翻译,其他还有摺积、叠积等,这些翻译的含义中总包含有混合、纠缠、重叠的意思,所以这种算法注定包含了充分混合得到新事物的过程。
卷积公式中反转坐标的意义
两个离散序列$x[n]$和$y[n]$,它们的卷积运算定义为:$$f[n]=x[n]*y[n]=\sum^{\infty}_{k=-\infty}{x[k]y[n-k]}=\sum^{\infty}_{k=-\infty}{x[n-k]y[k]} \tag{1}$$
我们观察卷积公式 $(1)$ 里,相乘的两项$x[k]$ 和 $y[n-k]$ 的下标有一个特点,就是$x[k]$ 和 $y[n-k]$ 下标之和总等于 $n$ . 所以,卷积公式 $(1)$ 可以用语言描述为
卷积函数 $f[n]$ 下标 $n$ 的值 ,等于所有下标之和等于 $n$ 的 $x[n]$ 和 $y[n]$ 乘积之和。
上面这句这个描述中,$x[n]$ 和 $y[n]$ 是平等、可互换的,所以卷积运算满足交换律。两个原始序列下标的配对过程如下图:
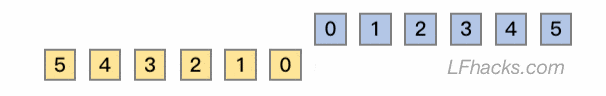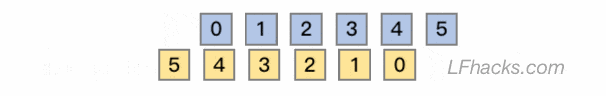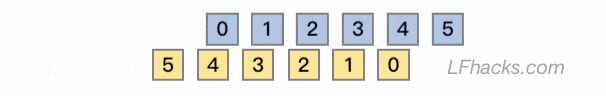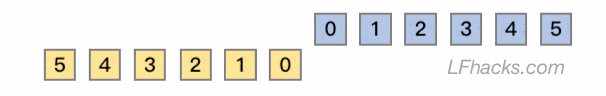
这就是卷积公式 $(1)$ 里,坐标反转的意义。
举个例子, 若将卷积函数记为 $f[n]$ ,那么 $f \left[ 5 \right] $ 的值等于所有下标之和等于$5$的 $x$ 和 $y$ 序列乘积之和:
$$ f \left[ 5 \right] = \cdots + x \left[ 0 \right] y \left[ 5 \right] + x \left[ 1 \right] y \left[ 4 \right] + x \left[ 2 \right] y \left[ 3 \right] + x \left[ 3 \right] y \left[ 2 \right] + x \left[ 4 \right] y \left[ 1 \right]+\cdots $$
反转的本质是取齐
上一节 提到,反转坐标的目的是找到所有下标之和等于 $n$ 的原始序列,这样做的本质是在自变量 $n$ 的维度里取齐。
- 如果自变量 $n$
是时间,那么就是在时间上取齐;比如同一时刻到达终点的运动员个数。

- 如果自变量 $n$
是一维空间坐标,那么就是在长度上取齐;比如同一个高度上观众的个数。

- 如果自变量 $n$
是二维空间坐标,那么就是在平面上取齐;比如同一个平面坐标点上的强度。
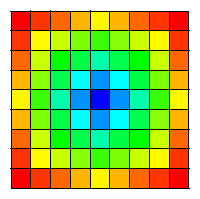
- 如果自变量 $n$ 是三维位置,那么就是在空间上取齐……

总结起来就是:
卷积就是两件事物相互合作,在同一个坐标点上共同施加的影响。
这里的共同施加,未必一定是如卷积公式 $(1)$ 中的先乘法再相加,只要是相互作用并得到新事物即可。
另一种视角:筛选
卷积公式 $(1)$ 除了 上面提到的共同施加影响 以外,还有另一种视角就是:一方 $x[n]$ 对另一方 $y[n]$ 的筛选,只有取齐了的结果才能放置在同一个坐标下。由于卷积满足交换律,所以这里的筛选并没有方向性,可以说 $x[n]$ 过滤了$y[n]$,同时也可以说 $y[n]$ 过滤了$x[n]$.
时间上的取齐
超市的例子
超市需要经常清理临近保质期的商品。如何在所有商品中,找到所有在今天到达保质期的商品?以我们的常识,应该是找出所有满足下面等式的商品:
生产日期 + 保质期 = 今天
例如,我们找出的商品可能如下表所示:
| 商品 | 生产日期 | 保质期 | 生产日期+保质期 |
|---|---|---|---|
| 方便面 | 2014-7-22 | 5年 | 2019-7-22 |
| 薯片 | 2017-7-22 | 2年 | 2019-7-22 |
| 酸奶 | 2019-5-22 | 2月 | 2019-7-22 |
| 面包 | 2019-7-20 | 2天 | 2019-7-22 |
对于任何一天 n,用上面的方法找出所有的失效商品,作为这一天的函数值:
| 失效期 n | 商品集合 f[n] |
|---|---|
| 2019-7-20 | 前天过期的商品集合 |
| 2019-7-21 | 昨天过期的商品集合 |
| 2019-7-22 | 今天过期的商品集合 |
| 2019-7-23 | 昨天过期的商品集合 |
| …… | …… |
得到的就是在不同日期 $x[n]$ 生产的商品,经过各自保质期 $y[n]$,筛选出特定某一天的过期商品集合。
空间上的取齐
波纹的例子
一滴水引起的波纹,波峰将形成什么形状?

水面所有质点都受同一个水滴激发,由于振动的相位只和到水滴的距离有关,所以到水滴相同距离的质点相位相同,得到圆形的波形。圆形的波峰是空间上取齐的集合。
杨氏双缝干涉的例子

双缝干涉的亮斑,是两个振动源的相位在空间上取齐的结果。
多个振动源干涉的例子
比 上面两个例子更广泛的例子,是多个振动源的相位在空间上取齐的结果。比如天线的方向图,就是多个振动源在空间取齐的结果。
时空上的取齐
下雨的例子
某一个时刻落在地面的雨滴数量,是什么决定的?

特定的出发位置、配合特定的出发时刻,让有缘分的雨滴在同一个时刻到达了地面。
交通的例子
同一条路上的人、车的集合,都是各自的出发地点、出发时间、和各自的路线、路上消耗的时间共同决定,最终在时间和空间上共同取齐的结果。

这些车在相同的时刻,聚到了相同的地点。
骰子点数之和的概率
正如 扔出两个骰子的点数之和 中表格所列,得到点数3的事件分解为:[1, 2] 和 [2, 1] 两种事件,就是两颗骰子能共同得到3的两种情况。
整数乘法
整数的乘法中包含了取齐求和的过程。比如:乘积里的十位,是由所有乘数里,能相乘得到十位数字的组合,取齐后相加得来。
1 2
x 3 4
------------
4 8
3 6 0
------------
4 0 8
上面的竖式里,乘积十位的 0 是由 4x10=40 和 30x2=60 相加得到的。如果用 反转平移 ,就能将更清楚的观看乘法过程。比如计算 12 x 34 = (10 + 2) x (30 + 4),下面例子里将 34 反转。
下面三幅图里,上面一行(10 2)向右运动,下面一行(4 30)向左运动。
10 2 ---->
▼
<---- 4 30
---------------
个位 8
10 2 ---->
▼ ▼
<---- 4 30
----------------
十位 40 + 60 = 100
10 2 ---->
▼
<---- 4 30
---------------------
百位 300
上面每一位都是两个乘数的各位取齐相加的结果。所以,整数乘法是卷积运算。
多项式乘法
作为整数乘法的抽象,多项式乘法同样是卷积。$$({x}+2)(3{x}+4) = (1 \times 3)x^2+(1\times4+2\times3)+(2\times4)$$
中学时候学的交叉相乘法求各项系数,
1 2
\ /
/ \
3 4
----------------------
6 + 4 = 10
其实是卷积运算的特殊情形,更一般的情况是反转-相乘-求和。比如求解下面的多项式 $$({x^2}+{2x}+3)(4{x^2}+5{x}+6)$$ 就应该对齐,比如上式中二次幂 ${x^2}$系数的求法:
1 2 3
6 5 4
----------------------
6 + 7 + 7 = 20
多项式乘法是 理解 Z变换 和 快速傅里叶变换 的起点。
信号与系统
卷积的理解往往是从《信号与系统》开始,但是《信号与系统》本身就是抽象的概念,并不能帮助理解卷积,反倒让人更加迷惑。了解了上面的多个例子以后,再看信号和系统函数的卷积,也许更能加深理解。
混响系统
唱 卡拉OK 的时候,会用混响系统来模拟回声效果:当你喊"喂”,它输出"喂(原声),喂(稍弱),喂(更弱)"……
所以当你唱歌的时候,你在任何一个时刻听到的其实是你的原声和多个更弱的回声相加的结果。
假设你唱的歌可以用 $x[n]$ 表示,那么加了混响后,你听到的歌用 $f[n]$ 表示:$$ f[n] = x[n] + a_1x[n-1] + a_2x[n-2] + \cdots + a_nx[n-n]$$ 由于回声一定比原声弱,所以这里$a_1,a_2, \cdots$ 应该是递减序列,例如下图所示
记作 $y[n]$ : $y\left[ 0 \right] = 1, y\left[1 \right] = a_1, y\left[2 \right] = a_2, \cdots, y[n]=a_n$. 如下图所示:
那么 $f[n]$ 可以重新写为:$$ f[n] = x[n]y\left[ 0 \right] + x[n-1] y\left[ 1 \right] + x[n-2]y\left[ 2 \right] + \cdots + x[n-n]y\left[ n \right]=\sum^{n}_{k=0}{x[k]y[n-k]}$$
与卷积公式 $(1)$ 完全相同。
信号和系统的互易性
正如 上节 所提到,由于卷积运算满足交换律,所以信号和系统的地位是相同的,你可以说是"信号"通过了"系统",也可以说是"系统"通过了"信号"。
举个例子:音响发烧友喜欢用名曲来检验音箱的优劣,就是在用同一个信号$x[n]$来处理不同音箱的系统函数$y[n]$.
和相关运算的区别
运算涵义
相关与卷积运算十分相似,都是两个集合的整体运算。由于位移方向和序列方向相同,所以对于两个序列来说,相关就是滑动点积,或者可以称为滑动投影。
$$R_{xy}[n]=\sum^{\infty}_{k=-\infty}{x[k] y[n+k]}$$
相关与卷积二者的差异在于:
- 卷积用来使两个集合相互影响,生成新的集合。
- 相关用来在一个集合中,寻找另一个集合的影子。
这一切的差异,仅来自一个正负号。
交换律
卷积满足交换律,而相关不满足。比如父亲和母亲共同的孩子,也可以说是母亲和父亲共同的孩子,并没有区别。用公式表示:
$$x[n] * y[n] = y[n] * x[n] $$
但是,如果把一个人的儿童和成人时期作对比:对于儿童来说,若干年 后 和成人长得完全一致;对于成人来说,则是若干年 前 和儿童完全一致。这一前一后,说明改变了相关的运算位置,得到的结果是不同且对称的,用公式表示:
$$R_{xy}[n] = R_{yx}[-n] $$
各位读后有什么想法,请在下方留言吧!如果对本文有疑问或者寻求合作,欢迎 联系邮箱 。邮箱已到剪贴板
精彩评论
本站 是个人网站,采用 署名协议 CC-BY-NC 授权。
欢迎转载,请保留原文链接 https://www.lfhacks.com/t/convolution/ ,且不得用于商业用途。

