从掷骰子观察二项分布

生活中的场景

生活中许多事情只有两种结果，而且需要反复多次尝试，比如：

小明要连续参加三次模拟考试，通过的标准是三次考试中有任意两次及格。假设小明每次考试通过的概率有1/6，想知道小明通过整个考试的概率有多少？

小明参加射箭比赛，如果每支箭射到靶上的概率为 p，那么当小明一共射出 N 支箭后，留在靶上有 k 只箭的概率有多少？

只有两种结果（例如 成功、失败）的实验，称为伯努利实验。那么做 N 次独立伯努利实验，任何一种结果（ 成功 或 失败）累计的次数，都符合二项分布。

这位伯努利，也是 伯努利双扭线 的那个伯努利，也是研究 对数螺旋的自相似性 的那个伯努利，同时是 伯努利定律伯努利定律 那个伯努利的大伯

我们把生活中这些例子抽象成掷骰子，来研究如何求解。

游戏规则

扔一次骰子的结果只有"是 6" 和 “不是 6” 两种结果，而且"是 6 “的概率为 1/6.

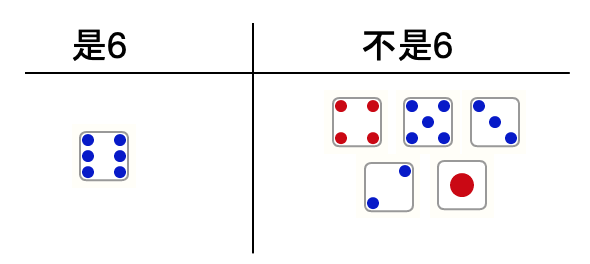
如果一把扔出 N 个骰子（或者一个骰子连续扔 N 次），将投出6的事件记为成功，累计成功的次数也就是 的个数记为 k，则 k 服从（N, p）二项分布。

比如，如果一把投出12颗骰子（N=12），得到如下图中的结果：

上图中， 共出现了3次，此次实验的结果 k=3

k 取值最大只能到 N，即一把扔出的骰子全部是 （666啊）；最小值是0，即一把扔出的骰子全部不是 （这个概率似乎大的多）。

那么 k 最可能取的数字是几？取到这个数字的概率又是多少？我们把 k 的可能取值列在下面的表里

二项分布就是研究这个 k 值的分布。下面我们用程序模拟几种特殊情况。

6的个数

我们用程序模拟扔出12个骰子，观察 k 的分布（k 是12个骰子中，6 的个数）。

点击"开始模拟"按钮，观察实验的过程： —-— —

模拟运行结果大概是下面这图的样子：

根据二项分布的理论，得到 k 个 6（或者1~6任何一个数字，p=1/6）的概率如下图形状：

可以看出和理论的分布形状是接近的。

4,5,6 其中任一

我们继续用程序模拟12个骰子扔出去，这次我们改变 游戏规则，只要出现4，5，6其中任一个都算成功。由于每个骰子出现4，5，6其中任一个的概率是1/2，所以p=1/2。

根据二项分布的理论，得到 k 个（4,5,6 其中任一，p=1/2）的概率如下图，我们：

下面用程序模拟 k 的分布，观察是否和理论一致。

点击"开始模拟"按钮，观察实验的过程：

模拟运行结果大概是下面这图的样子：

可以看出和理论的分布形状是接近的，而且接近了 正态分布。

二项分布的直观演示

高尔顿钉板 可以用来直观的演示二项分布的形状。

各位读后有什么想法，请在下方留言吧！如果对本文有疑问或者寻求合作，欢迎 联系邮箱 。邮箱已到剪贴板

精彩评论