从掷骰子得到正态分布

中心极限定理

中心极限定理表明，大量独立的同分布的随机因素，如果各项因素都不能起到主导作用，那么这些因素的共同影响结果，就服从正态分布。

一组独立同分布的随机变量$\{X_i\}$，无论其分布是什么，只要数量足够多，其总和$\Sigma X_i$逼近正态分布。

1颗骰子每次投出的点数，可以看做是独立同分布。我们用掷骰子的游戏模拟中心极限定理，进而得到正态分布。

游戏规则

当只有1颗骰子时，骰子的点数符合均匀分布。当扔出多次骰子时，每次骰子点数的总和，会随着试验次数的增多，接近正态分布。

我们下面用一次投出 N 颗骰子代替1颗骰子投出 N 次。

比如一次投5颗骰子，得到 [3,5,1,6,4] 的结果。那么所有骰子的总和为：$X=3+5+1+6+4=19$. 当骰子个数增加时，会发现 $X \sim N (\mu, \sigma)$

掷一颗骰子

一颗骰子每个面的概率相等。由于骰子有 6 个面，所以每个面的概率是1/6. 每个面的概率如下表：

面	1	2	3	4	5	6
概率	$1 \over 6$	$1 \over 6$	$1 \over 6$	$1 \over 6$	$1 \over 6$	$1 \over 6$

下图是模拟 600 次掷骰子的结果，点击"开始模拟"按钮开始模拟。柱状图显示了每个面出现的次数。能看出每个面出现的次数大致相等。

理论上均匀分布的概率分布图，用离散函数表示如下图，可以看出和上面实验结果类似。

掷二颗骰子

两个骰子面值之和的概率，是两个骰子各种组合的概率。

比如，得到点数3的概率为：一颗1、一颗2的概率 加上 一颗2、一颗1的概率 之和： $$ P(1)P(2) + P(2)P(1)=1/ 6 \times 1/ 6+ 1 /6 \times 1/6=1/18 $$

P (1)P (2)

P (2)P (1)

每个数值的概率如下表：

点数	2	3	4	5	6	7	8	9	10	11	12
概率	$1 \over 36$	$1 \over 18$	$1 \over 12$	$1 \over 9$	$5 \over 36$	$1 \over 6$	$5 \over 36$	$1 \over 9$	$1 \over 12$	$1 \over 18$	$1 \over 36$

上面表格内的概率值用离散函数表示，如下图所示，可以看出中间值 (7) 的出现概率最大，两侧数值的概率小。

从 卷积的直观解释 中我们可以知道，两个骰子的点数在特定值上取齐的概率，其实是两个骰子的概率质量函数 $P(n)$ 卷积的结果。

下图是模拟 2000 次掷两颗骰子的结果，点击"开始模拟"按钮开始模拟。柱状图显示了每个面出现的次数，投掷次数越多，越接近预测的概率分布。

模拟运行结果大概是下面这图的样子：

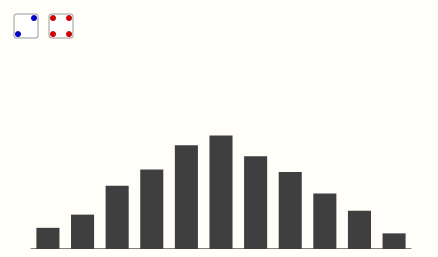
五个骰子

当骰子个数多起来之后，靠近中间值的概率越来越高，逐渐接近正态分布。下图是模拟 5000 次掷6颗骰子的结果，点击"开始模拟"按钮开始模拟。柱状图显示了每个面出现的次数，投掷次数越多，越接近正态分布。

模拟运行结果大概是下面这图的样子：

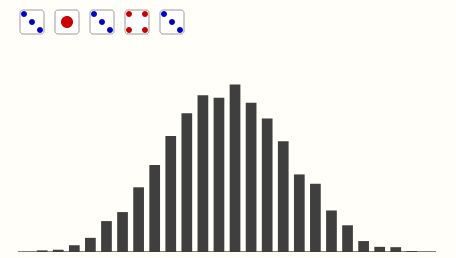
1万次投掷

当投掷次数多起来之后，模拟得到的频次统计，就越接近标准的正态分布。下图是模拟 10000 次掷12颗骰子的结果，点击"开始模拟"按钮开始模拟。柱状图显示了每个面出现的次数。

模拟运行结果大概是下面这图的样子：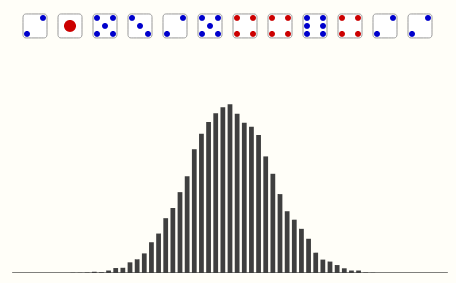

（完）

如果您对本文有疑问或者寻求合作，欢迎 联系邮箱 。邮箱已到剪贴板

精彩评论