本文用图形化的方式,演示使用傅里叶级数来展开方波的过程。
假设我们希望展开的方波的周期为 $T$,方波的频率为 $\omega_0 = {2\pi \over T}$

( ☝图片来源:http://fabmodules.com/fab2110-loading-your-input-transformer-square-wave-testing/ )
将方波函数记作 $f(t)$ , 下面我们来寻找如何用 傅里叶级数 来表示方波。
一般情况
方波的傅里叶级数有无穷多个项(因为突变那个位置有无限多的频率变化,可以想象为需要无穷多个圆润的正弦函数才能逼近尖尖的直角),也就是需要用无穷多个正弦函数表示。
$$ f(t) =\displaystyle\sum_{n=0}^\infin{A_n \sin(\omega_n t)}$$
其中数列 $A_n$ 和 $ \omega_n $ 是我们寻求的解,这二者都是无穷多项。还好,为了简化,我们让 $ \omega_n $ 表示为 某一个基频 $ \omega_0 $ 的 $n$ 倍,也就是:
$$ \omega_n= n \omega_0$$
这样形成的一族函数 $\sin(\omega_n t) $ 就是正交的,能极大的方便我们的运算。关于简谐函数的正交性可以参考这篇文字:简谐三角函数族。 在函数族: $\sin(n \omega_0 t) $ 中,频率为 $ n $ 倍基频 $ \omega_0 $ 的正弦函数称为 $ n $ 次谐波。
一次谐波
如果限定只用一个正弦函数来展开,为了让正弦函数尽可能的逼近原始方波,那必然使用频率和方波频率 $ \omega_0 $ 相同的正弦波表示,也就是基频函数:
$$ \hat{f}(t) = \sin(\omega_0 t) $$
为了更优雅、更本质的观察问题,我们决定升高一个维度,从实数域来到复数域,才能更清楚的理解这些问题的本源。使用的方法复杂了,结论就变得简单了。工具复杂了,留给使用者的只有简单了。
我们想象一个以基频 $ \omega_0 $ 速度旋转的复向量:
$$ e^{j\omega_0 t}$$
那么上面的正弦基函数就是这个复向量的实部(为了简单化,不再区分 $\sin(t)$ 和 $\cos(t)$)
$$ \hat{f}(t) = \sin(\omega_0 t) = \mathcal{Re}(e^{j\omega_0 t})$$
虽然我们眼中看到的世界只有实部,但是并不妨碍我们能从更高维度的空间来思考身边的世界。
下面的图展示了复向量的实部才是我们观察到的现象,反过来说,我们观察到的只是世界的一个侧面。
想象一个纸片人,生活在二维的纸片世界里:

我们用铅笔在纸片人旁边的纸上匀速画圆

那么这位纸片人看到的是什么呢?应该是下图这样
所以当纸片人希望研究这个黑点的坐标位置 $x(t) $ 随时间的变化规律时,便可以想象一个旋转的二维实向量的横坐标,而事实上也确实是更高维度世界里的一个圆。
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
——苏轼《题西林壁》
加入三次谐波
有了复向量的表示,上面的这个式子:
$$ f(t) =\displaystyle\sum_{n=0}^\infin{A_n \sin(n \omega_0 t)}$$
就可以重新表示为:
$$ f(t) =\displaystyle\sum_{n=0}^\infin{A_n e^{jn\omega_0 t}}$$
方波的谐波只有奇数谐波,也就是 $n$ 都是奇数,上一节 中限定只用一个正弦函数展开,本节再多加入一项,使用一次和三次谐波来逼近方波。
$$ \hat{f}(t) =A_1 e^{j\omega_0 t} + A_3 e^{j 3\omega_0 t} $$
其中向量的幅度 $A_1$ 和 $A_3$ 可以从傅里叶级数的推导计算得出,这里我们重点观察两个向量相加的直观表示。
复向量相加符合三角形法则:把第二个向量的起点放置在第一个向量的终点,第二个向量的终点就是得到的新的向量。
比如下图三个向量,满足矢量加法:
$$ \overrightarrow{a} + \overrightarrow{b} = \overrightarrow{c} $$
那么,上面这个式子:
$$ \hat{f}(t) =A_1 e^{j\omega_0 t} + A_3 e^{j 3\omega_0 t} $$
就是两个旋转的复向量首尾相连,而且其中一个是另一个旋转速度的三倍,也就是说其中一个转一周的时间内,另一个转完了三周,如下图所示:
图中的红点就是第二个向量的终点,也就是两个向量相加得到的和的位置,这个新向量的实部就是对方波的逼近: $ \hat{f}(t) $
当加入了三次谐波后,我们可以看到,这时的波形已经比一次谐波更接近方波了。
继续逼近
按照 上一节 中的规律,继续增加 五次、七次……等奇次谐波,可以观察到越来越接近方波。
逼近的方波在示波器上看到的效果:
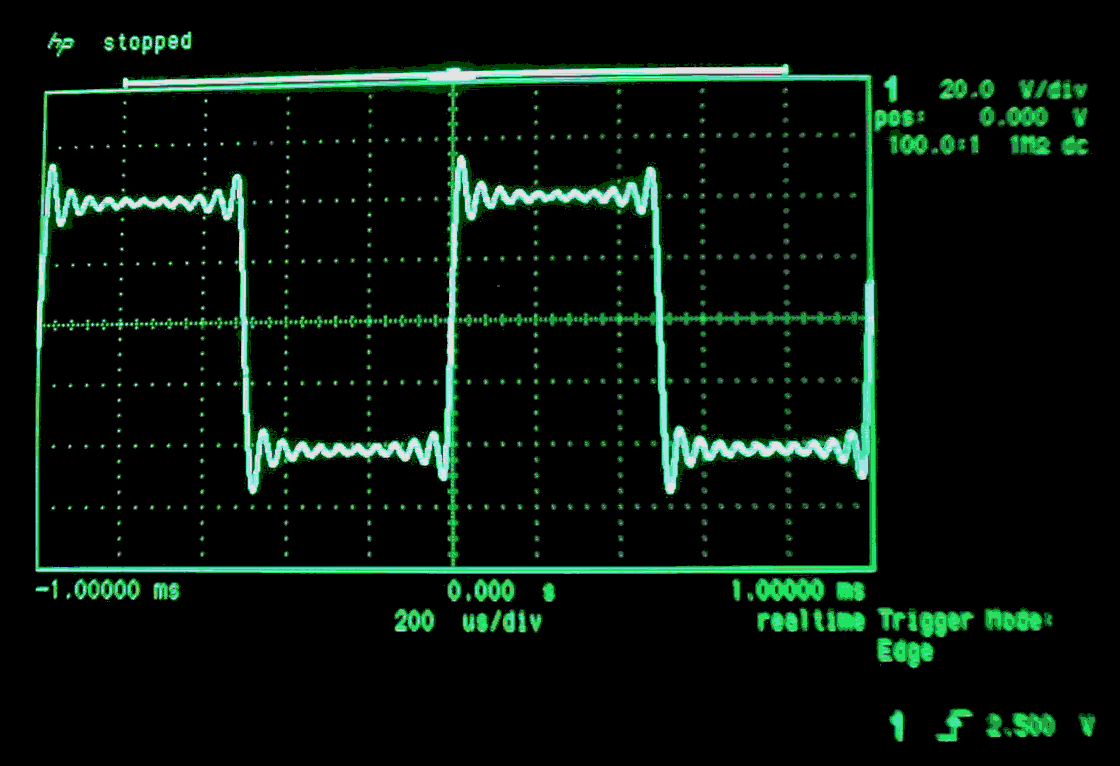
( ☝图片来源:http://www.trevormarshall.com/byte_articles/byte6.htm )
如果您对本文有疑问或者寻求合作,欢迎 联系邮箱 。邮箱已到剪贴板

