三角函数族

定义

谐波三角函数族，harmonically related sinusoidal functions，指一族拥有共同周期的正弦函数和余弦函数。其中拥有最长周期的函数称为基波，频率为基础频率$\omega_0$.函数族为$$\sin(\omega_0t),\sin(2\omega_0t),\sin(3\omega_0t),\dots,\cos(\omega_0t),\cos(2\omega_0t),\cos(3\omega_0t),\dots$$

下面图中显示了一组频率为$\omega_0,2\omega_0,3\omega_0,4\omega_0$的正弦函数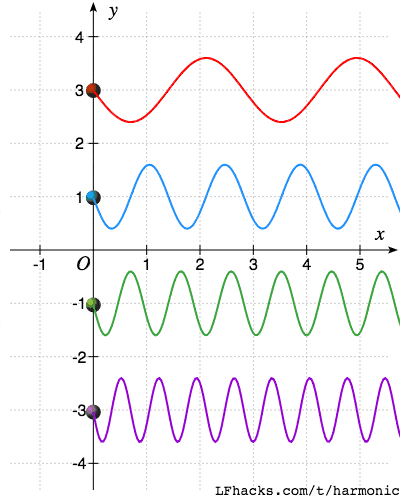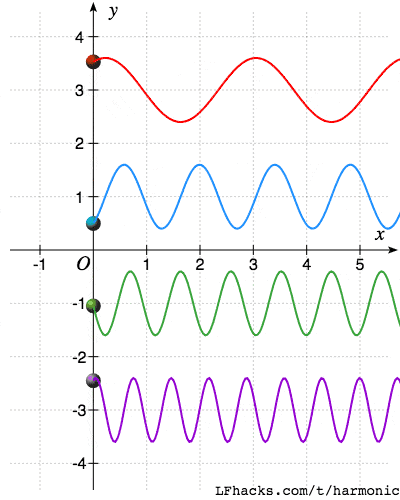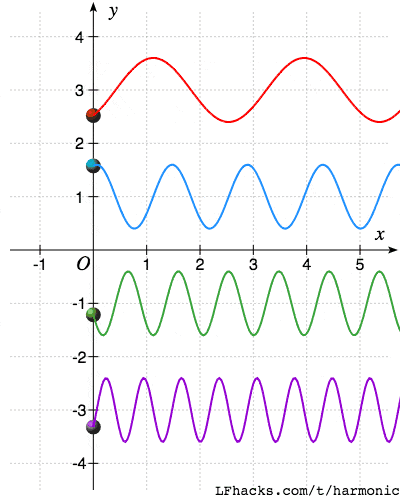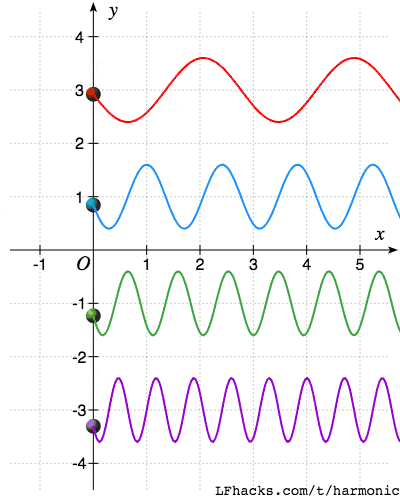

正交性

三角函数有个很有用的性质：正交性。含义是，任意不同频率的三角函数之积，在一个周期内积分为0.
比如我们看看一个周期内，乘积$$\sin(2\omega_0t)\sin(3\omega_0t)$$的图形：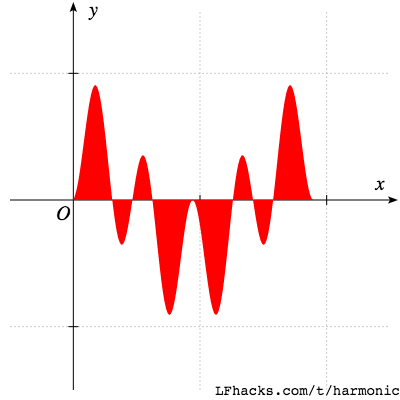

乘积$$\cos(2\omega_0t)\sin(3\omega_0t)$$的图形:

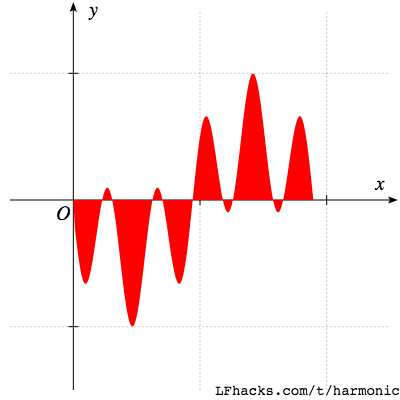
仔细观察可以看出，图形在 x 轴以上的部分和以下的部分，面积相等，所以整个周期内积分为0

这个性质，使三角函数被用作一组基函数，表示任意周期函数，也就是 傅立叶级数

如果您对本文有疑问或者寻求合作，欢迎 联系邮箱 。邮箱已到剪贴板

精彩评论