利萨如图形,Lissajous curve,也叫李萨如图形、李沙育图形,用来展示两个相互垂直的简谐振动的合成。两种垂直的振动可能是相互垂直的弹簧、或者相位相差 90°的正弦波信号。
动态演示
下面的动态图像,可以用来展示任意频率比例的利萨如图形。
使用方法
点击按钮:Restart(重新启动)或 Pause(暂停)按钮以改变演示状态
在右侧的控件中填入参数:
- 两个振子的频率 $a, b $,比如 $a=2, b=3$
- 相位 $ \theta, \delta $,比如 $ \theta=\pi/2,\delta=0 $
参数的几何含义见 这里
参数式
利萨如图形的参数方程式如下:
$$ x(t) = \sin(at+\theta), y(t) = \sin(bt + \delta) $$
几何含义为:有两个振子,振动方向相互垂直,振幅相等,振动频率分别为 $a$ 和 $b$,振子的瞬时位置为 $x(t), y(t)$,分别作为图形的横、纵坐标 $x$, $y$
式中的 $\theta$ 和 $\delta$ , 表示两个振子各自的初始相位。
利萨如图形的性质
上面 参数式 一节中的 $a$,$b$,$\theta$,$\delta$ 强烈影响着 利萨如图形利萨如图形的形状,在上面的动态演示中可以 通过控件来改变 它们的值。
频率比
$a$ 与 $b$ 的比值 $a/b$ ,是决定利萨如图形状的首要因素, 强烈影响着利萨如图形的动态演示利萨如图形的形状。比如:
- 当 $a/b$ 为有理数时,图形曲线闭合
- 振动频率之比决定图形在$x$, $y$方向上的叶瓣的个数
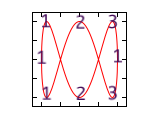
比如,$a:b=1:3$ 时,得到的图形如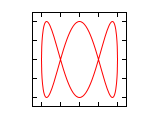
图中 $x$ 横轴方向上的叶瓣有1个,而 $y$ 纵轴方向上的叶瓣有3个
相位差
随着相位差 $\phi = \theta-\delta$ 的变化,图形看起来像在三维空间旋转的投影。下面观察几种参数组合的图形:
| 频率比 a/b | 相位差 φ | 利萨如图形形状 |
|---|---|---|
| 1:1 | 0° | 直线 |
| 1:1 | 0°~90° | 椭圆 |
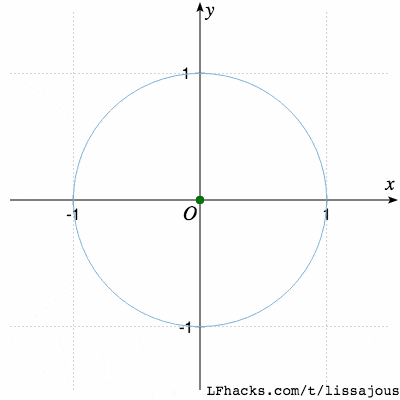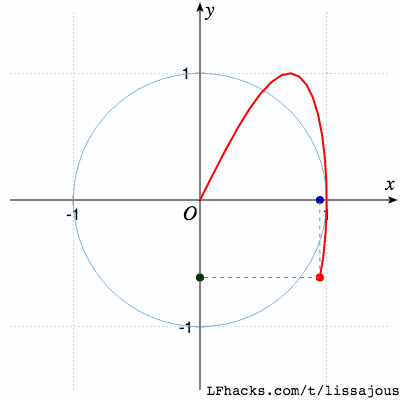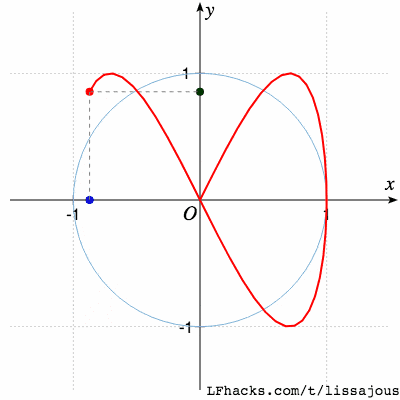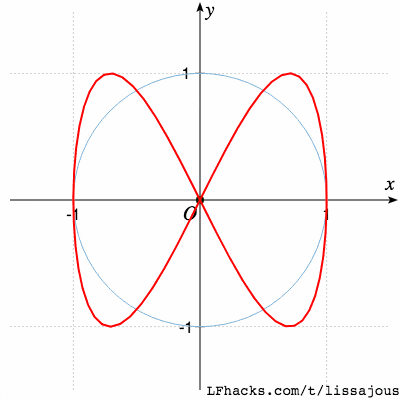
| 1:1 | 90° | 圆 |
a:b=1:1
最简单的情形,完全同相,$\phi=0$得到直线
$\phi= \pi/4$ 得到椭圆
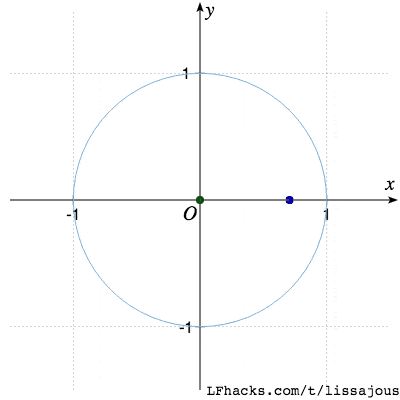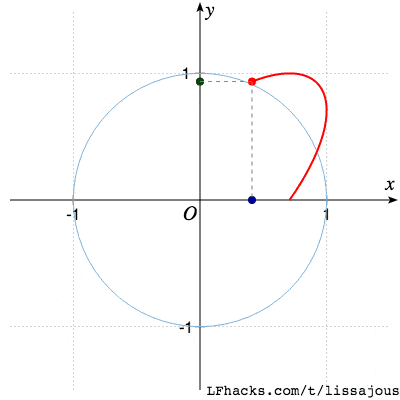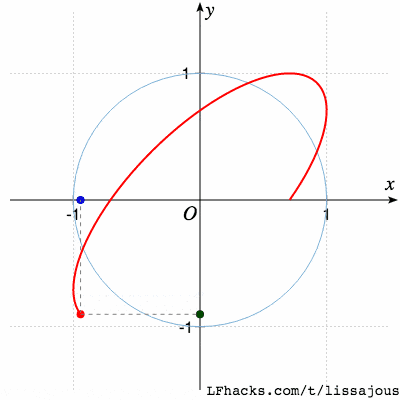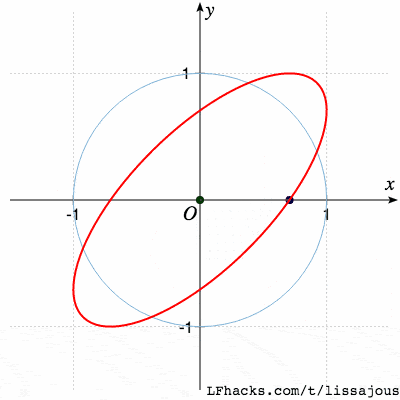
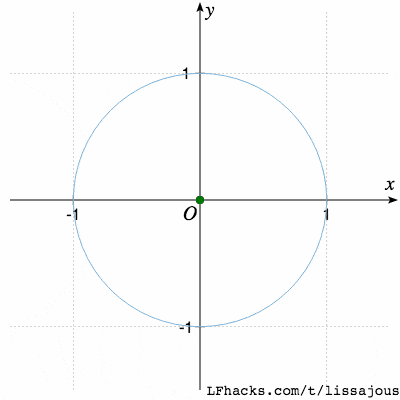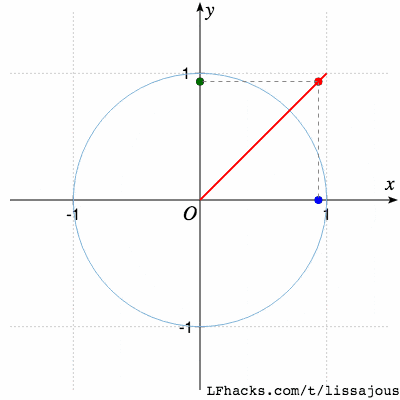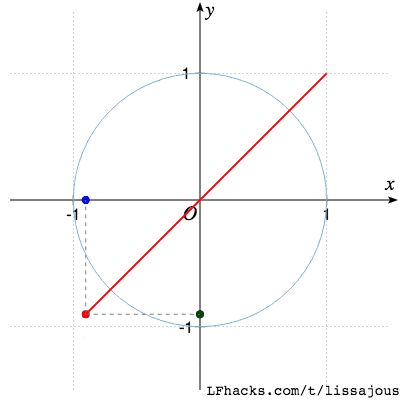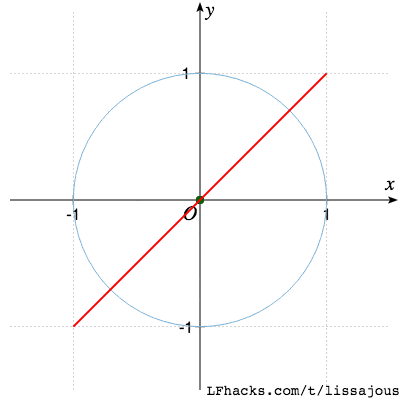
$\phi= \pi/2$ 得到圆(从参数式看出,$\sin$ 函数移相 $\pi/2$ 得到 $\cos$,于是图形是圆 )
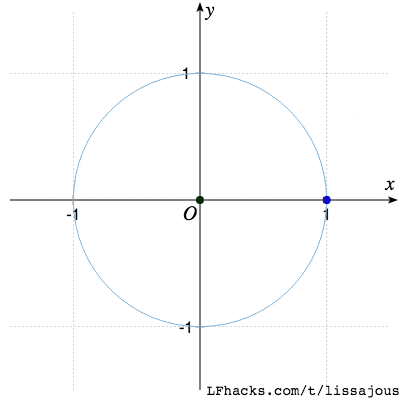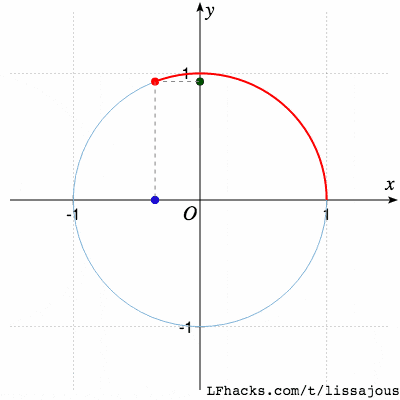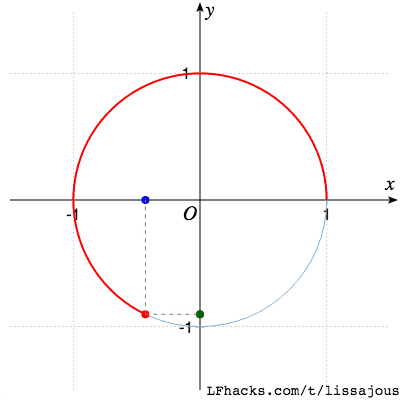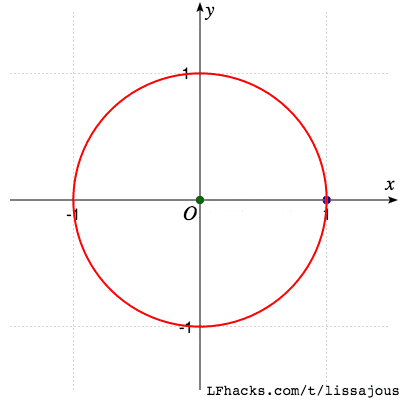
(这一步是由两个振子得到圆,和 正弦函数 中、圆分解为两种振动的过程刚好相反)
当 $0 \le \phi \le 2\pi$ 时,图形的变化趋势如下图:
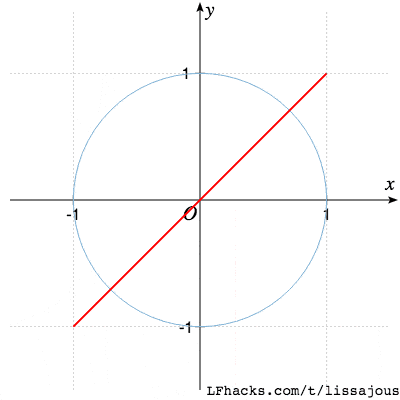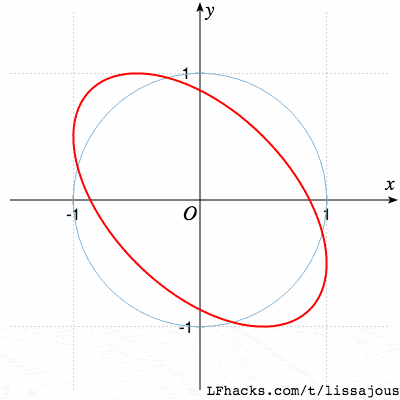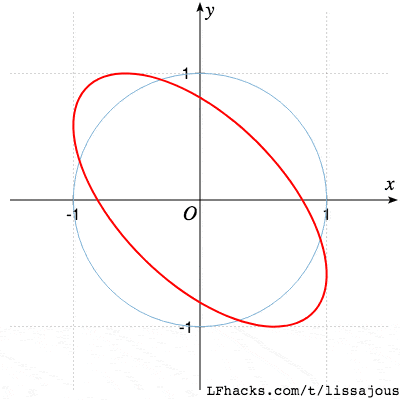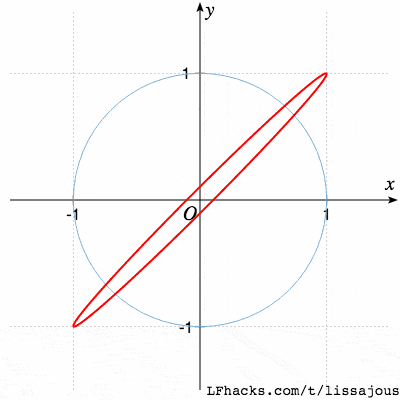
图形好像一个圆绕着圆柱旋转时,在屏幕上的投影。
有没有感觉像下面的 旋转舞者?一会觉得是向左转,一会觉得是向右转。

a:b=1:2
如 这里 所讲,a 值决定 y轴 方向的叶瓣数量,b 值决定 x轴 方向的叶瓣数量。
$\phi=0$得到蝴蝶形状:
$\phi = \pi/4$得到单根曲线:
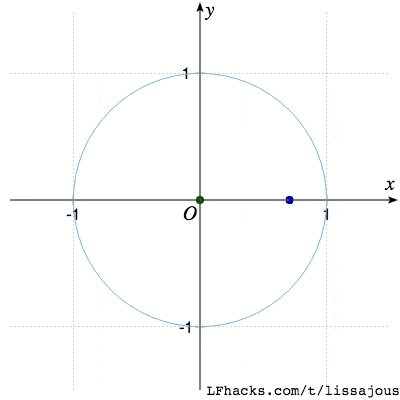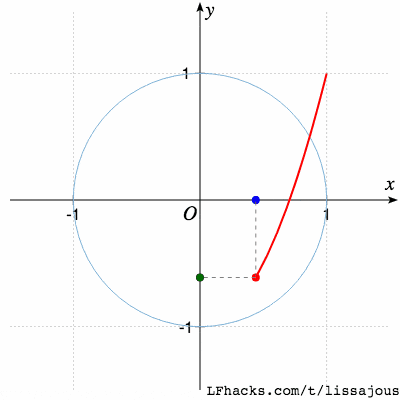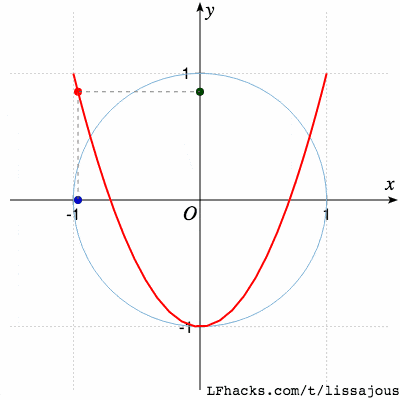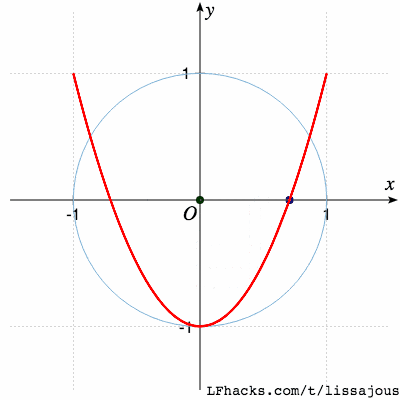
$\phi = \pi/2$又得到蝴蝶形状,不同的只是起始点位置:
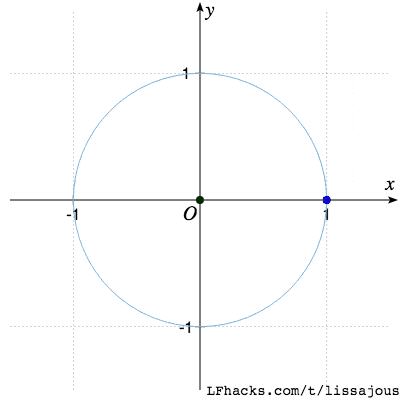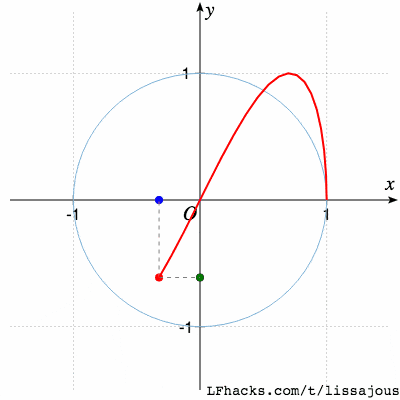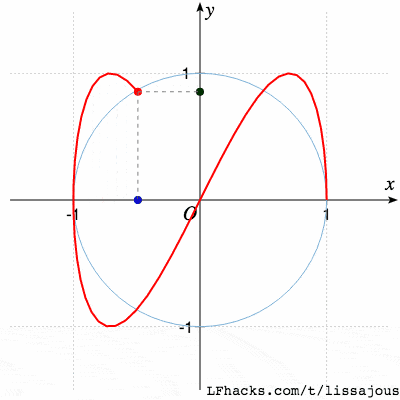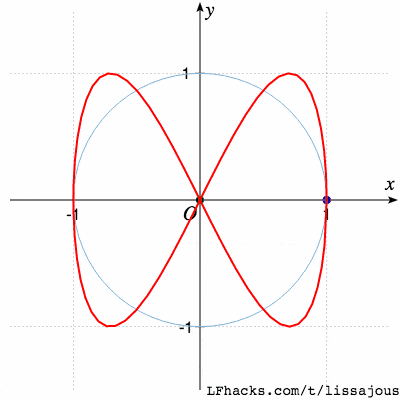
当 $0 \le \phi \le 2\pi$ 时,图形的变化趋势如下图:
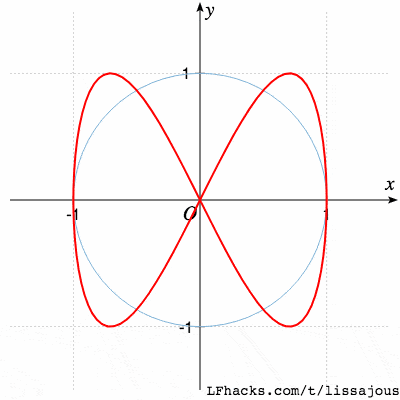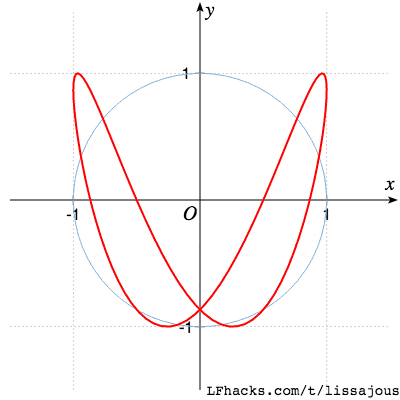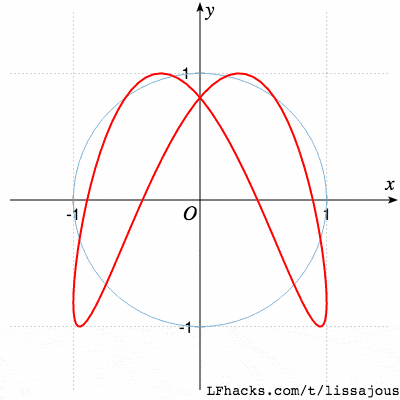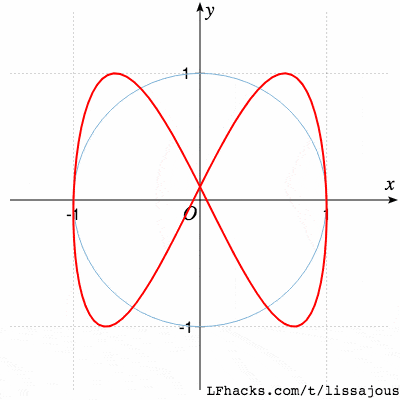
其他 a:b 值
本节展示多种频率比值条件下,相位差在 $0 \le \phi \le 2\pi$ 范围改变时图形的变化过程。
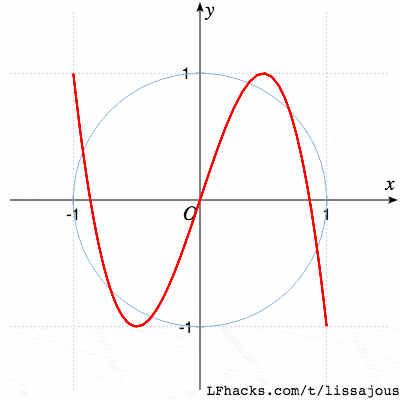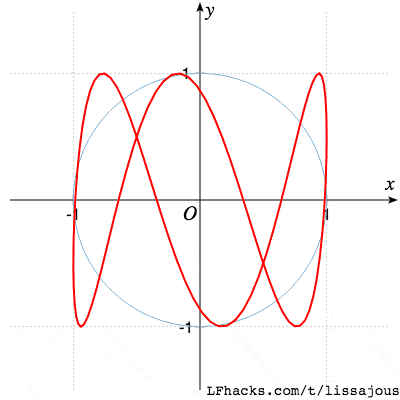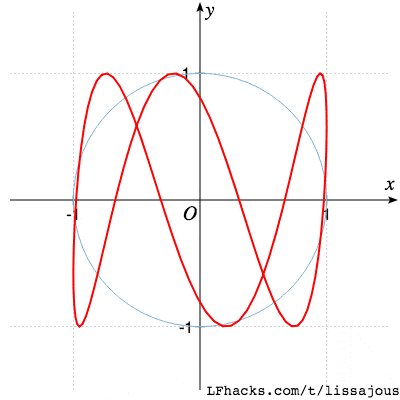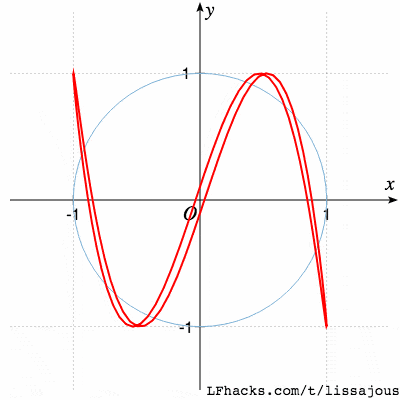
$$a:b=1:3$$
$$a:b=2:1$$
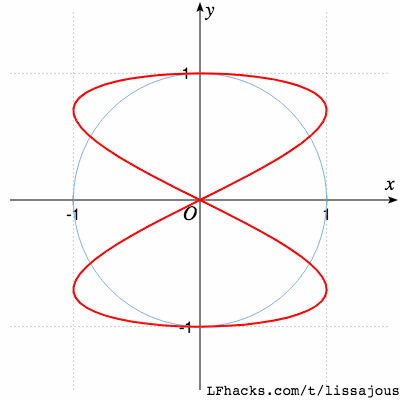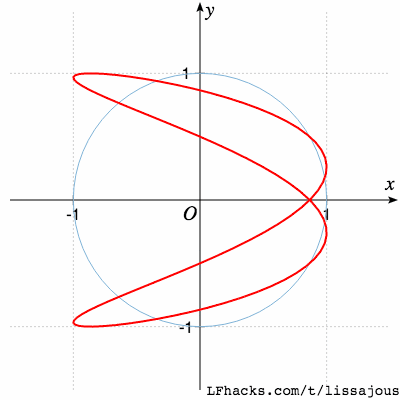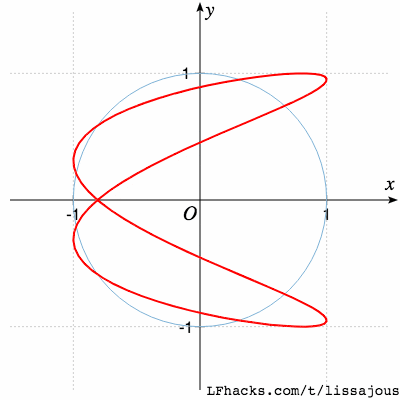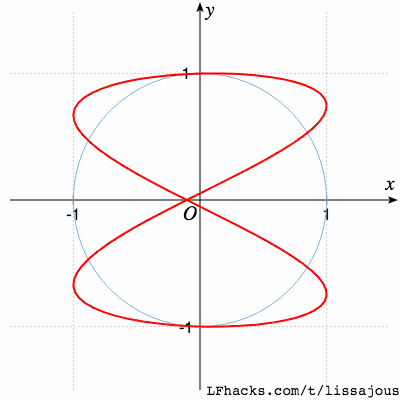
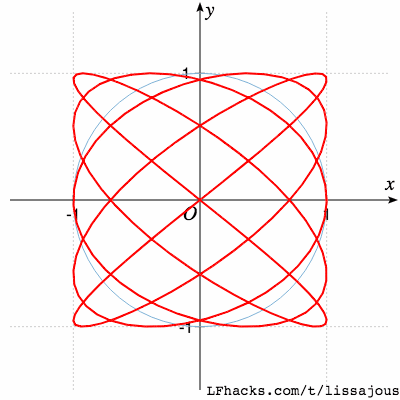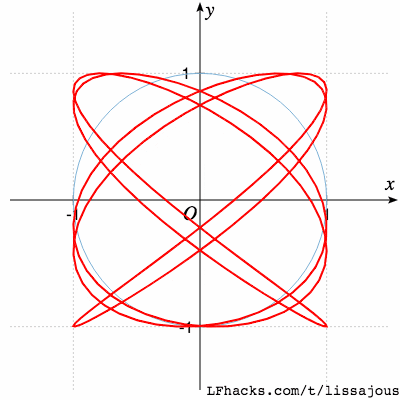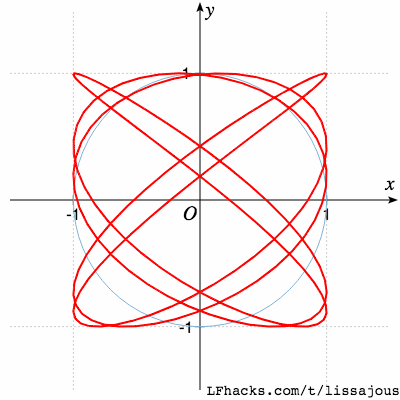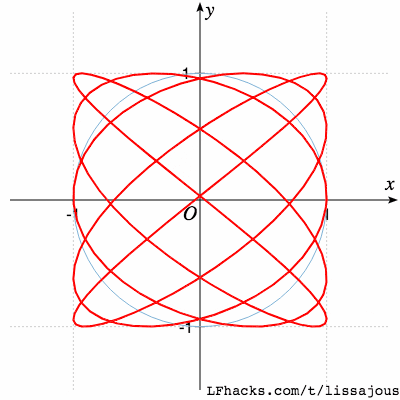
$$a:b=5:4$$
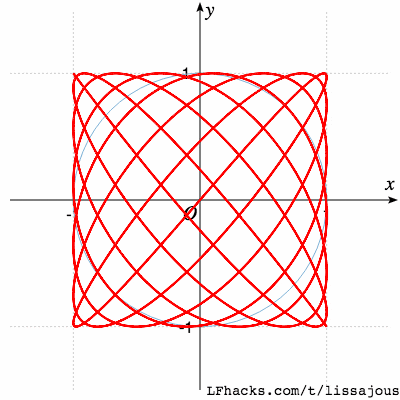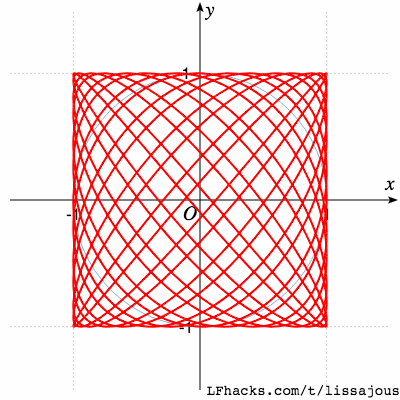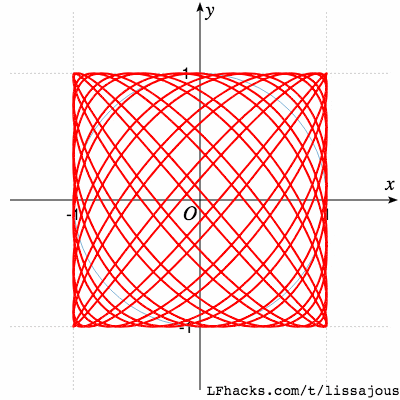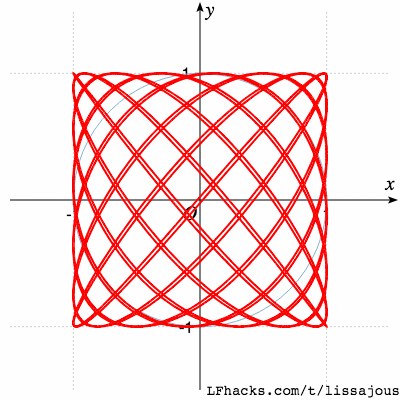
$$a:b=13:15$$
各位读后有什么想法,请在下方留言吧!如果对本文有疑问或者寻求合作,欢迎 联系邮箱 。邮箱已到剪贴板
精彩评论
本站 是个人网站,采用 署名协议 CC-BY-NC 授权。
欢迎转载,请保留原文链接 https://www.lfhacks.com/t/lissajous-curve/ ,且不得用于商业用途。

