抛物线

抛物线的定义

抛物线是一种圆锥曲线

抛物线上的点，与一个点F（称为焦点）之间的距离等于到固定直线L（称为准线）之间的距离。

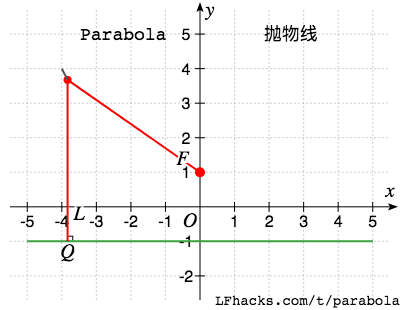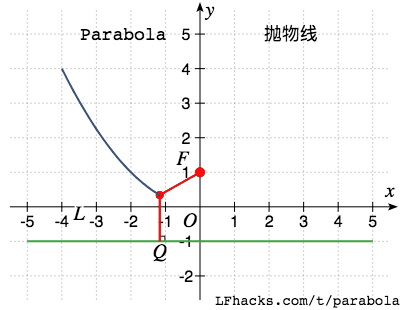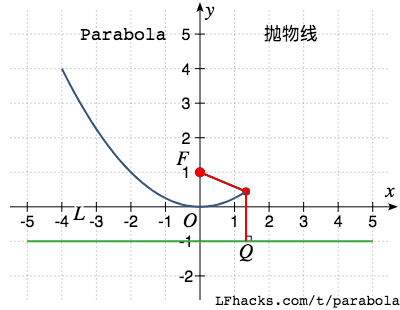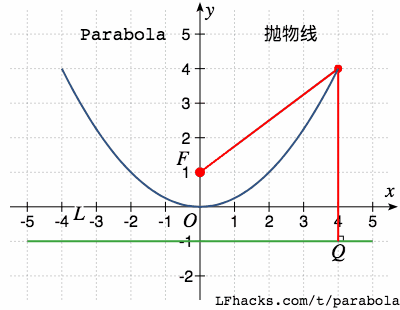
二次项系数的影响

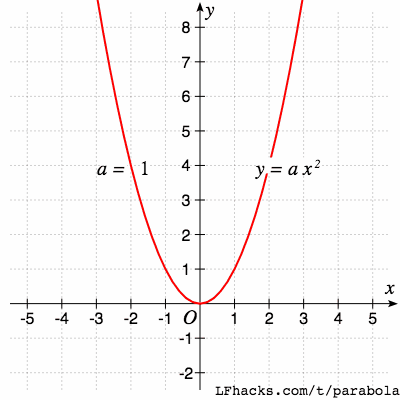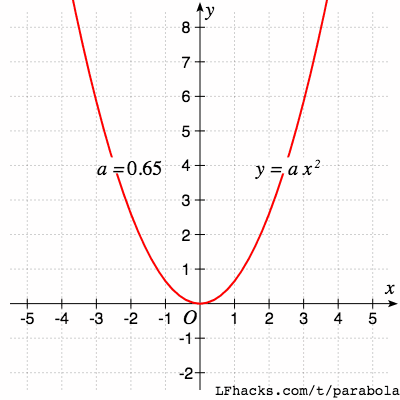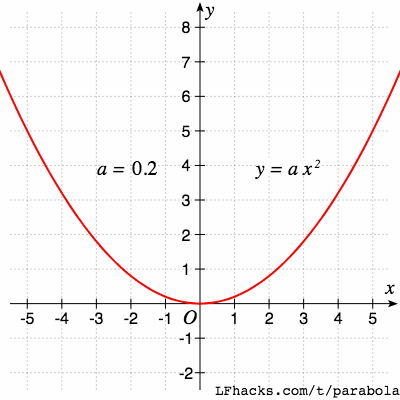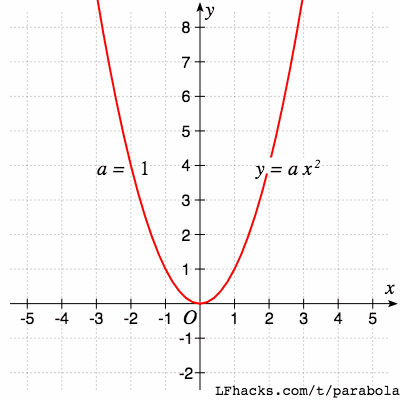
对于标准形式的抛物线 $y = ax^2 + bx +c$ ，二次项系数 $a$的符号决定了抛物线的开口方向，$a$ 的绝对值决定了抛物线的开口大小。

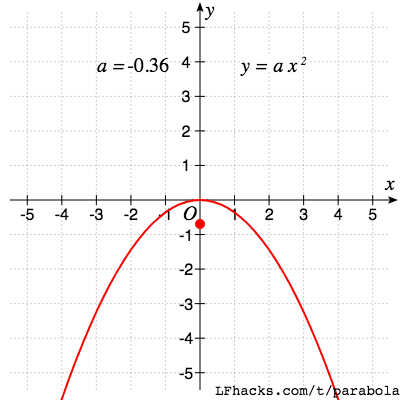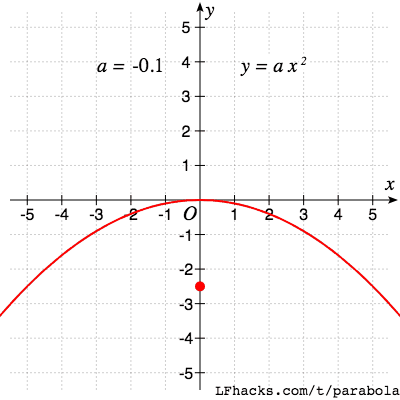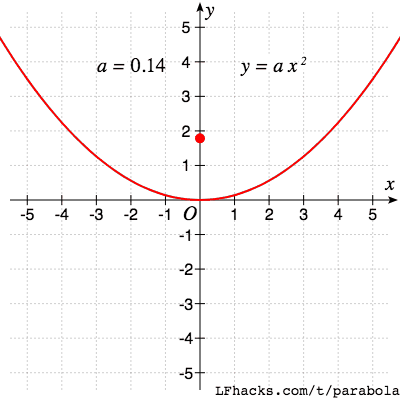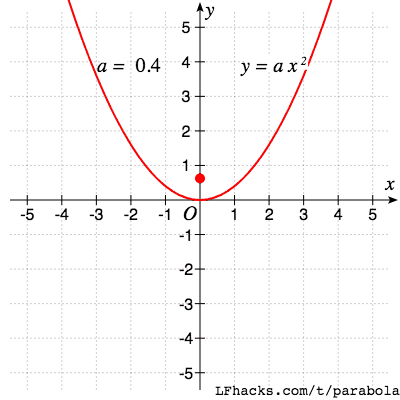
抛物线开口变大的同时，焦点也越来越远。可以想象，当 $a = 0$ 时，焦点在无穷远处，开口反向后，焦点从另一侧回到原点附近。

一次项系数的影响

一次项系数 $b$ 决定了抛物线顶点的位置，随着 $b$ 的改变，抛物线顶点的路径也是一个抛物线。

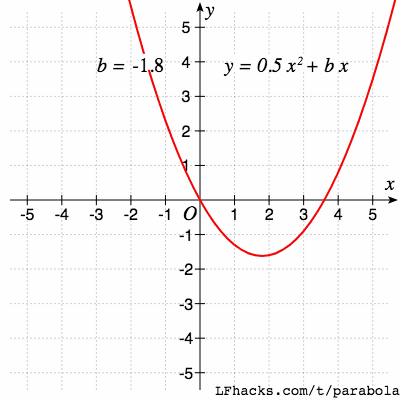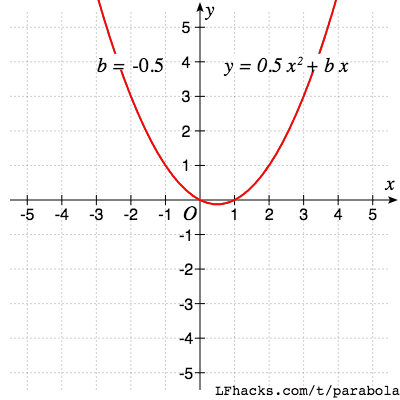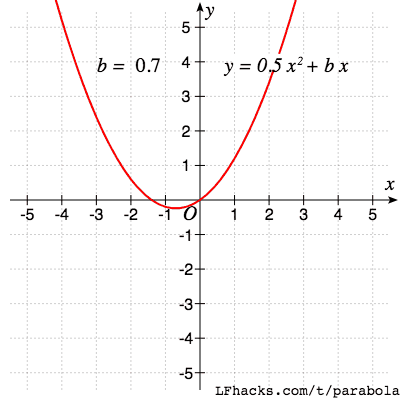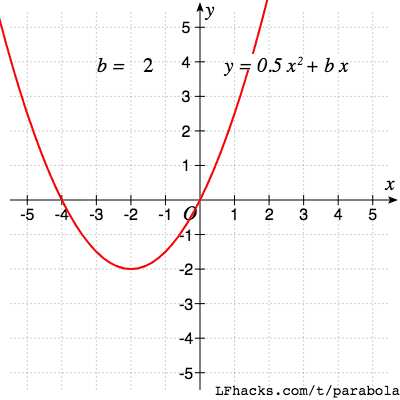
单位抛物线

正如所有圆都是相似的，所有抛物线也都是相似的。正如圆有 单位圆 ，也有单位抛物线：

$$y = x^2$$

任意抛物线可以平移或者缩放得到单位抛物线，也就是：

$$y’ = a (y + b)\\x’ = a (x + b)$$

反射性质

所有圆锥曲线，具有以下反射性质：

平行于对称轴的光线，将汇聚在焦点处。

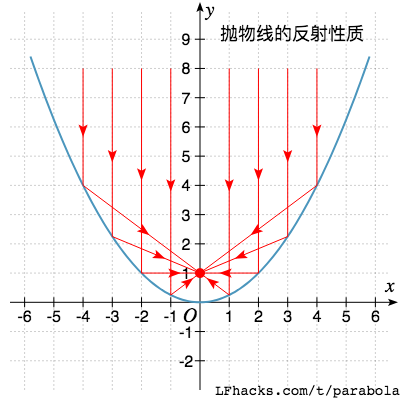
可以认为抛物线的另一焦点位于无穷远处。

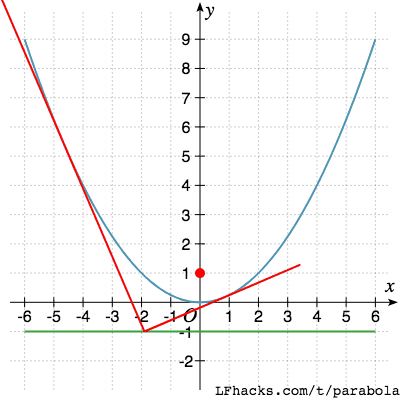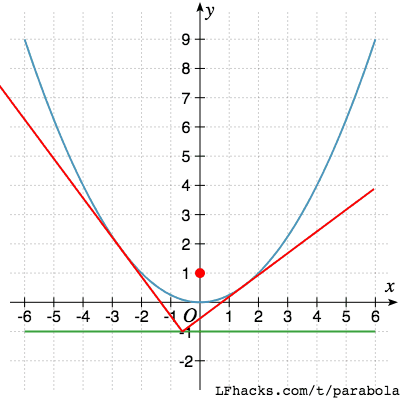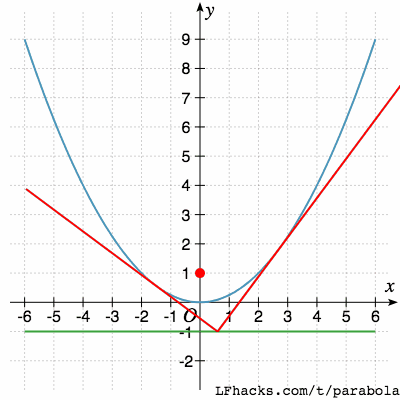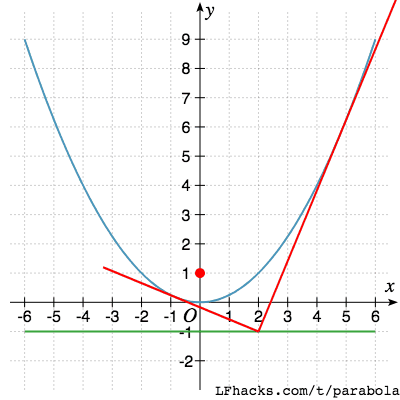
Orthoptic 性质

抛物线相垂直的两条切线，垂足位于准线上

反之亦成立

抛物线两条相交于准线上的切线，相互垂直

如果您对本文有疑问或者寻求合作，欢迎 联系邮箱 。邮箱已到剪贴板

精彩评论