勒洛三角形的互动演示

在 为什么阴井盖是圆的？ 这篇文章中提到，除了圆形以外，勒洛三角形状的阴井盖也不会掉入下水道。

绘制方法1

首先我们来看如何作出一个 勒洛三角形的互动演示，其实只需要一个圆规就够了。

步骤：

1. 以任意点（如下图中的 红点 ）为圆心，画一个圆心角超过 60° 的圆弧（如下图中的 红色 圆弧）；
2. 以相同的半径，在第一个圆弧上靠近端点的任意点（如下图中的 绿点 ）为圆心，画出第二个圆弧（如下图中的 绿色 圆弧）；
3. 以上面两段弧的交点（下图中的 蓝点 ）为圆心，保持半径不变，作出第三个圆弧（如下图中的 蓝色 圆弧）；
4. 三段圆弧形成的封闭图形即为 勒洛三角形

绘制方法2

第二种方法是以正三角形为基础

1. 作一个正三角形
2. 分别以三个顶点为圆心、以顶点的对边为弦作弧，三段弧围成的封闭图形即为 勒洛三角形勒洛三角形

定宽曲线

试着用两条平行线去夹一个封闭曲线，保证两条直线只从外部接触到曲线，有一个交点而不穿过它。如果无论从哪个角度去夹，这两条平行线的距离保持不变，那么这个封闭曲线就叫做定宽曲线，平行线之间的距离称为定宽曲线的宽度。

（图片来自网络）

圆的周长 这篇文章展示了 圆 作为定宽曲线，在滚动时的形态。还可以把鼠标放在下图的圆上，感受一下定宽曲线：

勒洛三角形勒洛三角形也属于定宽曲线。把鼠标放在下图的勒洛三角形上，感受一下定宽曲线：

勒洛多边形

宽度相等的定宽曲线组成了一个家族，称为勒洛多边形。和 正三角形类似，勒洛多边形是以奇数条边的正多边形为基础制作出来的。有些国家的硬币 就采用勒洛七边形。

下图展示了勒洛三角形和勒洛五边形，不妨把同宽度的圆也一起放进来做个对比。因为正多边形随着边数的增多能逼近圆，勒洛多边形也同时在逼近圆。

周长

我们把 定宽曲线 中定义的宽度记为 $d$，然后来寻找定宽曲线的周长 $C$ 与宽度 $d$ 的关系。如下图所示：

勒洛三角形每段弧的半径 $ R=d $ ，圆心角等于正三角形的一个内角 $60\degree$ 所以勒洛三角形的周长为 $$C=3 \cdot \frac{2\pi d}{6}=\pi d $$

上图中，右侧的圆的宽度同为 $d$ ，它的周长也是 $\pi d$。其实，所有宽度相同的定宽曲线的周长都是相等的：

Barbier 定理：所有宽度为 $d$ 的定宽曲线的周长都等于 $\pi d$

面积

宽度为 $d$ 的勒洛三角形的面积公式： $$ A=\frac{1}{2} (\pi - \sqrt{3})d^2 \approx 0.7 d^2 $$

与之宽度相等的圆面积：$$ A=\frac{\pi}{4}d^2 \approx 0.785 d^2 $$

宽度为 $d$ 的 勒洛多边形中，面积最小的是勒洛三角形，面积最大的是圆。勒洛三角形和圆的面积位于 勒洛多边形 的两个极端。

方孔钻头

勒洛三角形的每个内角都是 120°，是所有 勒洛多边形 中最小的内角，也意味着是最"锋利"的角。所以如果用作切割刀具，首选勒洛三角形。

方孔钻头的工作过程如下图：

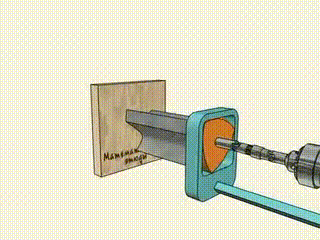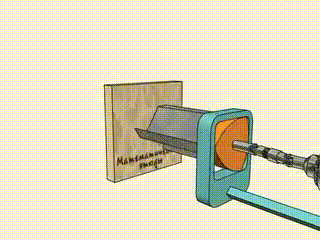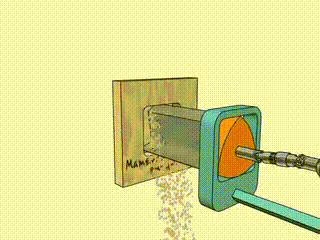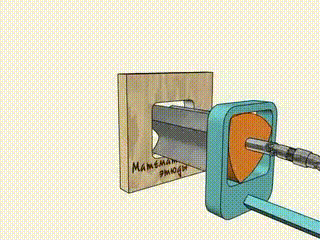
Wankel 发动机

Wankel 发动机也叫转子发动机，和奥拓发动机不同的是，其中的转子的截面采用了勒洛三角形。

（图片来自网络）

有人利用 TikZ 在 Tex 样例页面 上发布了一个例子，展示了 Wankel 发动机的做功过程。简单的动图如下：

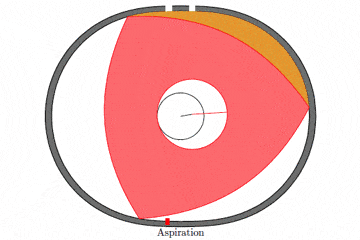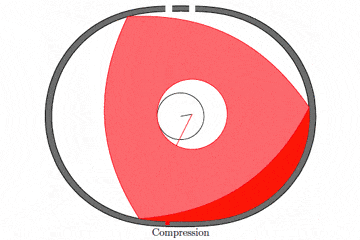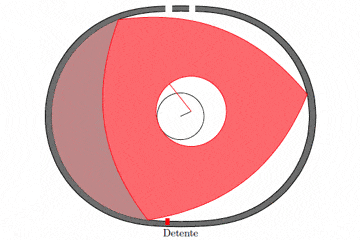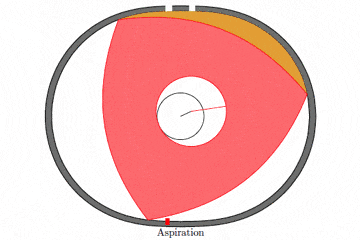
图上各冲程的名词解释：

• Aspiration：吸气
• Compression：压缩
• Explosion：爆炸
• Detente：减压
• Echappement：排气

为什么不能当轮子

既然如 定宽曲线 一节所展示的，类似圆和勒洛三角形这种定宽曲线可以在平行线间随意滚动。那么为什么只有圆可以作轮子，而没有见过使用 勒洛三角形 作轮子？

原因是这样的：一个曲线能作轮子，要求并不是曲线的宽度保持一致。而是要求轮子的轴到地面的距离恒定。因为车身是固定在轮轴上的，保持车身稳定是基本的要求。

在 勒洛多边形 中，勒洛三角形是中心对称性最差的，需要旋转120°才能和自身重合，所以用 勒洛三角形 做的轮子是最颠簸的。

把鼠标放在下图上，感受一下 勒洛三角形 用作轮子时，车身的颠簸。

生活中的勒洛多边形

在我们生活中，是否能看到 勒洛多边形 的身影？

裁缝用的划粉片

（图片来自网络）

上海某建筑的平面图

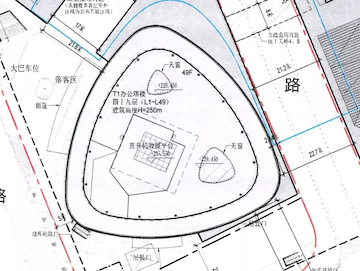
（图片来自网络）

贝斯、吉他的拨片

（图片来自网络）

硬币

英国 50便士 硬币

（图片来自网络）
硬币轮廓采用 勒洛多边形 后，仍然能保证硬币通过自动贩卖机的分拣通道，因为在平行直线中滚动时，勒洛多边形和等宽的圆形没有什么区别。下图展示了分硬币的过程，图中可以看出硬币在平行通道中滚动的样子。

（图片来自网络）

如果您对本文有疑问或者寻求合作，欢迎 联系邮箱 。邮箱已到剪贴板

精彩评论