窗户的定价规则

背景

窗户一般由两种材料组成：型材和玻璃。型材用于组成窗框，玻璃用于填充窗户。

窗户的报价是按成品窗的面积乘以单价计算。其中玻璃的面积是随着窗户面积成正比增加的，但是型材的成本是和长度成正比的，按照窗户面积计算价格，会不会随着窗户的增多，潜在的利润会越大？下面做一番推导。

模型

窗户是以扇为单位的。假设我们每扇窗的高度为 $a$，宽度为 $b$，那么每扇窗户的面积为 $$ab$$

另假设一共有 $n$ 扇窗户，那么，窗户的总面积为 $$nab$$

玻璃的增长关系

随着窗户数量的增长，所需玻璃的数量呈线性的增长，每单位面积的窗户消耗的玻璃数量为玻璃面积 $A_{玻璃}$ 除以窗户面积 $A_{窗户}$

$$C_{玻璃} ={A_{玻璃} \over A_{窗户}} = {nab \over nab } = 1$$

窗框的增长关系

接着看所需窗框的长度，这是问题的关键。我们关心随着窗户 $n$ 的增大，窗框型材所需的量会如何增长。

制作 $n$ 扇高度为 $a$，宽度为 $b$ 的窗户，所需的窗框型材由两部分组成：

1. $n$ 扇窗户所需的窗框长度为 $2(a+b) \cdot n$
2. 一个整体的外框： $2(a+nb)$

所以，$n$ 扇窗户所需的窗框型材总长度为：

$$\begin{align} L_{型材} &= 2(a+b) \cdot n+2(a+bn) \\ &= 2an+2bn+2a+2bn \\ &= 2(a+2b)n+2a\end{align}$$

所以随着窗户数量的增长，每单位面积的窗户消耗的窗框型材长度为：型材的长度除以窗户面积

$$\begin{align} C_{型材} &={L_{型材} \over A_{窗户}} \\ &= {{2(a+2b)n+2a} \over {nab}} \\&= {{2(a+2b) \over ab}+{2 \over {nb}}}\\ &={{2 \over b}+{4 \over a}+{2 \over nb}} \end{align}$$

是由常数项 ${{2 \over b}+{4 \over a}}$ 和 倒数项 ${2 \over nb}$ 组成。随着 $n$ 的增大，这两项谁占优势决定了窗框成本的趋势。

窗框的成本趋势

接下来我们看看倒数项 ${2 \over nb}$ 的占比，来推断这两项之和随着 $n$ 增长的趋势如何

$$\begin{align}\rho(n) &={{2 \over nb} \over {{2 \over b}+{4 \over a}+{2 \over nb}}} \\ &={{2a \over nab} \over {{2an+4bn+2a}\over{nab}}}\\ &={{a}\over {(a+2b)n+a}} \end{align}$$

取一个比较合理的窗户尺寸比例 $a=2b$，那么上式变为

$$\begin{align}\rho(n) &={{a}\over {(a+a)n+a}}\\&={{1}\over {2n+1}}\end{align}$$

画出函数图形为

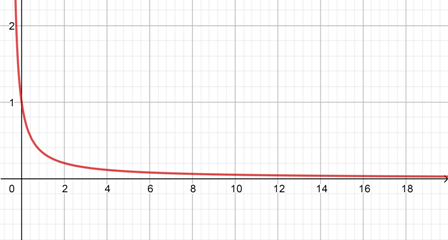
结论

结论1

可以看出，当窗扇的个数 $n$ 增多时（一般正常的数量在10以上），倒数项的占比非常小（<0.1），所以窗框型材成本和成品窗户的面积成正比，这个比值是$${{2 \over b}+{4 \over a}}$$ 所以结论1是

当听到店主统一按面积计算价格时，你就可以放心了。

结论2

窗框型材成本$${{2 \over b}+{4 \over a}}$$里，$a$和$b$都在分母上，所以结论2是

所以当窗户面积小时，供应商往往会限制窗户的最小面积，或者提高单价。反过来，$a$和$b$增加时，单位面积的成本会降低，所以落地窗的成本相对更低。

结论3

窗高 $a$ 的系数是4，对相对窗宽$b$成本的影响更大，所以有时候会限制 $a$ 的最小值，类似"高度不到 1m 按 1m 算"这种算法。

（完）

如果您对本文有疑问或者寻求合作，欢迎 联系邮箱 。邮箱已到剪贴板

精彩评论